Created by potrace 1.15, written by Peter Selinger 2001-2017 Yuze Zou's HomePage 🇨🇳

Pop-Art算法复现

 
  • Yuze Zou
  • 2019年 09月28日
  • 0 阅读

通过PyTorch实现Pop-Art算法。

前言

Learning-values-across-many-orders-of-magnitude1一文中提出了Pop-Art算法以解决深度强化学习(Deep reinforcement learning)中target值跨度多个量级而造成的学习缓慢的问题。其中Pop与Art分别表示Preserving Outputs Percisely以及Adaptive Rescaling Target, 即在保障已历经样本输出不变的前提下自适应缩放target值的算法。更为详尽的介绍在论文翻译: Learning values across many orders of magnitude中已给出, 在此不再赘述。本文的目的在于复现论文中提到的算法, 以测试其有效性, 并为适用于自己的问题服务。本文通过PyTorch实现, 结构如下: 首先验证PyTorch的核心组件以测试模型拆分的等效性(这将作为后续的基础); 接着实现PopArt算法与Normalized SGD算法(论文中的算法1, 2)并验证二者的等效性(论文2.3节的statement); 最后通过复现第三章中的示例(包括另外两种对比算法)以期复现论文中的Fig. 1a。

Show me the code

GitHub repo: zouyu4524/Pop-Art-Translation

验证PyTorch核心组件

首先, 验证对PyTorch几个核心组件(backward, step, forward)的理解是否有误。为此, 设计两组网络结构如下:

  • 由LowerLayers + UpperLayer组成
  • UnifiedModel是以上两部分堆叠而成

LowerLayers结构如下:

class LowerLayers(torch.nn.Module):
    def __init__(self, n_in, H):
        super(LowerLayers, self).__init__()
        self.input_linear = torch.nn.Linear(n_in, H)
        self.hidden1 = torch.nn.Linear(H, H)
        self.hidden2 = torch.nn.Linear(H, H)
        self.hidden3 = torch.nn.Linear(H, H)

    def forward(self, x):
        h_tanh = torch.tanh(self.input_linear(x))
        h_tanh = torch.tanh(self.hidden1(h_tanh))
        h_tanh = torch.tanh(self.hidden2(h_tanh))
        h_tanh = torch.tanh(self.hidden3(h_tanh))
        return h_tanh

UpperLayer结构如下:

class UpperLayer(torch.nn.Module):
    def __init__(self, H, n_out):
        super(UpperLayer, self).__init__()
        self.output_linear = torch.nn.Linear(H, n_out)
        torch.nn.init.ones_(self.output_linear.weight)
        torch.nn.init.zeros_(self.output_linear.bias)

    def forward(self, x):
        y_pred = self.output_linear(x)
        return y_pred

需要对比的是这两种网络在初始权重|训练集一致的情况下, 通过各自定义的loss, optimizer执行相应的backward和step操作后, 权重的更新是否仍然一致。如果理解无误, 那么两个网络在更新后, 对应层的权重参数应该仍然一致。

两种模式的对比

  • LowerLayers + UpperLayer模式
lower_layer = LowerLayers(16, 10)
upper_layer = UpperLayer(10, 1)

opt_lower = torch.optim.SGD(lower_layer.parameters(), lr)
opt_upper = torch.optim.SGD(upper_layer.parameters(), lr)

loss_func = torch.nn.MSELoss()
loss = loss_func(upper_layer(lower_layer(sample_x)), sample_y)

loss.backward()
opt_lower.step()
opt_upper.step()

注意: 其中两部分分别设置了optimizer, 相应传入的参数为各自网络的参数(opt_lower为lower_layer.parameters(), opt_upper为upper_layer.parameters()); 而在计算loss时, 仍然按照顺序连续计算出预测的y, 与标的的y计算均方差。如此, 在调用loss.backward()时将分别计算出loss对两个网络各层参数的梯度。而更新权重时, 需要分别调用各自 optimizer 的 step() 函数完成参数更新。

  • UnifiedModel 模式
unified_layer = UnifiedModel(16, 10, 1)

loss_func = torch.nn.MSELoss()
loss = loss_func(unified_layer(sample_x), sample_y)

loss.backward()

with torch.no_grad():
    for para in unified_layer.parameters():
        para -= lr * para.grad

此处未设置optimizer, 手动实现SGD的step函数。

Tips: 控制PyTorch复现的方式是在调用任何PyTorch相关函数前设置torch.manual_seed()。

实验结果

对比两组实验的结果分别如下:

  • LowerLayers + UpperLayer 模式
Parameter containing:
tensor([[ -6.5463,  14.0888,  14.7738, -21.8954,  11.8038,  -9.8505,  -1.7764,
         -27.6084,  26.4289,  22.8444]], requires_grad=True)
Parameter containing:
tensor([85.1712], requires_grad=True)
  • UnifiedModel 模式
Parameter containing:
tensor([[ -6.5463,  14.0888,  14.7738, -21.8954,  11.8038,  -9.8505,  -1.7764,
         -27.6084,  26.4289,  22.8444]], requires_grad=True)
Parameter containing:
tensor([85.1712], requires_grad=True)

其中打印的分别是最后一层的权重和bias完全一致(第一种模式中相当于UpperLayer的参数, 第二种模式中相当于UnifiedModel最后一层的参数)。

此外, 对于底层(LowerLayers)的参数也同样是一致的(结果在此略过)。

小结

通过两组实验的对比, 明确了PyTorch中的几个关键函数backward, step, forward的使用方式。与此同时, 将网络拆分为两部分的测试有助于实现Pop-Art算法(其核心思路是将网络最后一层分离, 进行normalization后再做训练)。

杂项

separate_model.py中commented部分还包括对backward的输入参数grad_tensors的测试。该参数作为所求梯度的权重对应乘上, 即含义为被求导变量的前序梯度。与tensorflow中的tf.gradients的第三个参数grad_ys功能一致。该参数默认为标量1。因为一般而言, 被执行backward的变量为标量。而实际也可以对向量执行backward, 相应地若要考虑其前序梯度则需要在该参数填上与向量维度一致的Tensor。

PopArt算法实现

论文中共给出了两个算法: 1) Pop-Art 和 2) Normalized SGD, 并证明了两个算法的等效性。
本节分别实现这两种算法并验证其等效性。

算法概述

  • 算法1: Pop-Art

Pop-Art

如图, 算法1中的关键在于对UpperLayer(即参数W和b)的两次更新, 其中第一次是自适应scale(即ART)的同时保留已训练样本的结果(即POP)。第二次是优化算法下的参数更新。需要注意的是: 第一次的更新仅改变参数值(.data), 不改变参数的梯度(.grad)。另一方面, 有了上一节中拆分网络的经验, 算法1中对两层网络的梯度计算也可以归并为一步loss.backward()计算。再分别通过各自网络的优化算子(optimizer)调用step()更新参数。

  • 算法2: Normalized SGD

Normalized-SGD

如图, 算法2的关键是通过缩放后的目标差值和UpperLayer的权重参数更新LowerLayers的参数。为了实现这一点, 我们需要暂时地放缩UpperLayer的权重数值(.data)以及目标差值。同样地, 调用loss.backward()将计算两层网络的梯度, 其中UpperLayer的梯度不受缩放的影响(因为梯度中无W), 但权重数值本身被缩放, 需要在完成梯度计算后还原。

注意: 这里有一个重要的trick。即缩放|还原UpperLayer的权重数值时务必使用in-place的方式: 即W.data *= scalar这样, 原因在于这种操作方式不会变更W.data在内存中的物理地址, 因而计算梯度(backward)时, 通过计算图寻到的W, 其中的W.data便是更改后的结果。否则, 如果采用非in-place的更新方式, 如W.data = W.data * scalar, 那么实际上新开辟了一个内存地址, 存储更新后的W.data, 而计算梯度时, 通过计算图找到的W中的W.data实际上仍然是原来的W.data2。更为详尽的说明与分析在PyTorch backward 与 in-place 赋值小记中给出。

实验结果

分别实现以上两种算法后, 进行对比测试: 两种算法分别以相同的随机数种子初始化两层网络权重, 对比单步的网络更新后LowerLayers网络的权重变化。结果如下:

  • 以LowerLayers各层的bias对比来看
# 算法1: Pop-Art
tensor([-0.1496, -0.1486, -0.2989,  0.0683, -0.1775, -0.2820,  0.2773, -0.2053,
        -0.0360,  0.0906])
tensor([ 0.2812, -0.0810,  0.1392,  0.2818,  0.1046,  0.3161,  0.1640,  0.1966,
        -0.1107,  0.1517])
tensor([-0.0687,  0.0421,  0.1568, -0.2215,  0.2655, -0.0343, -0.2649, -0.1710,
         0.2799,  0.2893])

# 算法2: Normalized SGD
tensor([-0.1496, -0.1486, -0.2989,  0.0683, -0.1775, -0.2820,  0.2773, -0.2053,
        -0.0360,  0.0906])
tensor([ 0.2812, -0.0810,  0.1392,  0.2818,  0.1046,  0.3161,  0.1640,  0.1966,
        -0.1107,  0.1517])
tensor([-0.0687,  0.0421,  0.1568, -0.2215,  0.2655, -0.0343, -0.2649, -0.1710,
         0.2799,  0.2893])

可见两种算法下更新后的LowerLayers各层参数完全一致。另一方面, 由于两种算法对UpperLayer的处理方式不同, 其权重更新后有所不同, 但两个算法最后给出的predict结果则如下:

# 算法1: Pop-Art
tensor([3.9995])

# 算法2: Normalized SGD
tensor([3.9995])

结果完全一致, 印证了论文2.3节中的Proposition 3。

结果复现

有了以上的准备工作, 可以着手复现文章第三章中给出的对比三种算法测试实验。

数据集与测试方法

数据集的输出为0 ~ 1023的随机数, 输入为对应输出的二进制表示(16位, 高位补0); 而为体现异常值的影响, 每1000个随机数后设置1个65535(即16位全1)。全体数据集一共5000个样本。

验证算法的指标为 RMSE, 即均方根误差。具体而言, 数据集顺次逐一喂入模型, 在训练前先测试当前样本在已有模型上的误差(Test Error, 绘图所用的误差结果即该值的序列), 而后以此样本训练模型, 更新模型参数。如此直至所有样本参与训练。

算法实现小结

论文中给出了三种对比算法, 分别是SGD, ART以及PopArt, 对比如下:

Alg. 说明
SGD 传统的gradient decent方法, 对数据集不做任何标准化处理
ART 在SGD的基础上, 跟踪更新统计量(数据集的均值与方差), 并对输出进行标准化, 但对UpperLayer的参数无特殊处理, 即不保障已训练样本的输出不变
PopArt 在ART基础上, 还结合了POP, 即更新统计量, 对输出标准化的基础上, 对UpperLayer参数进行修正以保障已训练样本的输出不变

实际上, 对比三个算法的差异, 结合算法1中的流程, 可以一套代码实现三个算法, 差异仅仅在于以下两步:

\[\begin{aligned} {\bf ART:~ } &\mu_t = (1-\beta_t) \mu_{t-1} +\beta_t Y_t ~ \text{and}~\sigma_t^2 = \nu_t - \mu_t^2,~\text{where}~\nu_t = (1 - \beta_t) \nu_{t-1} + \beta_t Y_t^2\\ {\bf POP:~ } &{\bf W}_ \text{new} = {\boldsymbol \Sigma}_ \text{new}^{-1} {\boldsymbol \Sigma} {\bf W} \quad \text{and} \quad {\boldsymbol b}_ \text{new} = {\boldsymbol \Sigma}_ \text{new}^{-1} \left( {\boldsymbol \Sigma b + \mu - \mu}_ \text{new} \right) \end{aligned}\]

那么, 对应的不同的算法只需要跳过相应的环节即可。最后实现的效果关键代码如下:

ART与POP功能分别划分为独立的执行单元:

def art(self, y):
    self.mu_new = (1. - self.beta) * self.mu + self.beta * y
    self.nu = (1. - self.beta) * self.nu + self.beta * y**2
    self.sigma_new = np.sqrt(self.nu - self.mu_new**2)

def pop(self):
    relative_sigma = (self.sigma / self.sigma_new)
    self.upper_layer.output_linear.weight.data.mul_(relative_sigma)
    self.upper_layer.output_linear.bias.data.mul_(relative_sigma).add_((self.mu-self.mu_new)/self.sigma_new)

在网络前向传递的过程中根据算法种类确定ART与POP单元的调用情况。

def forward(self, x, y):
    if self.mode in ['POPART', 'ART']:
        self.art(y)
    if self.mode in ['POPART']:
        self.pop()
    self.update_stats()
    y_pred = self.upper_layer(self.lower_layers(x))
    self.loss = 0.5 * self.loss_func(y_pred, self.normalize(y))
    return y_pred

杂项

算法中给出的LOSS函数为1/2 * MSE, 为此我们需要注意在定义LOSS函数时乘以0.5, 以复现论文中的结果。

结果

对应三种算法采用的参数如下表所示:

Alg. $\alpha$ (learning rate) $\beta$
SGD $10^{-3.5}$ NaN
ART $10^{-3.5}$* $10^{-4}$
PopArt $10^{-2.5}$ $10^{-0.5}$

* 论文中给出的是$10^{-2.5}$, 但实际结果发现$10^{-3.5}$更贴近论文图示中所给出的结果。

在以上的参数设置下, 最后得到的结果如下图所示:

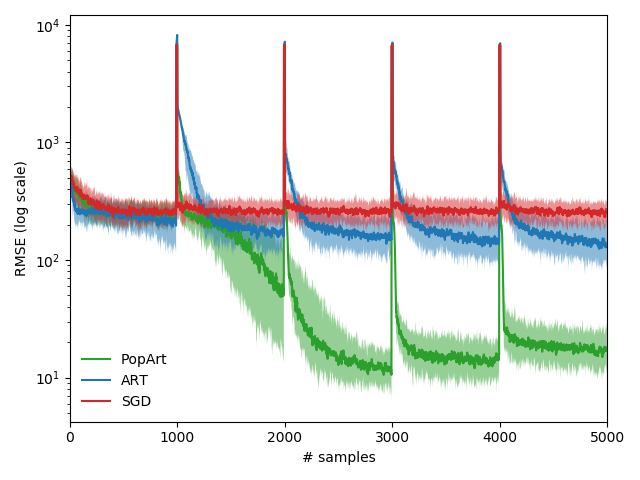
compare

与论文中的图对比可以发现, PopArt, SGD算法的结果基本一致, ART算法的趋势也基本一致, 但绝对数值上略有区别。

  1. Learning-values-across-many-orders-of-magnitude ↩

  2. What is the recommended way to re-assign/update values in a variable (or tensor)? ↩

搜索