暴力求解小游戏。“闲不过系列”。
动机
最近玩到了一款手机游戏,名字叫做 Calculator: the Game,游戏玩法很简单,通过给定的操作符在给定的步数以内将原始的数字变换到目标数。起初的一些关卡较为容易,但是后续的关卡短时间内无法想到求解思路,所以产生了“暴力求解”的想法。为了快速实现需求,采用Matlab实现。

Demo
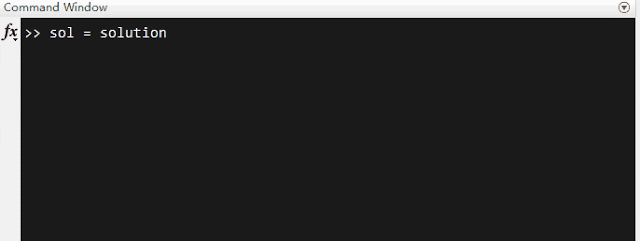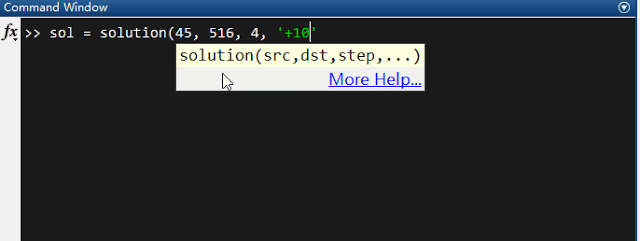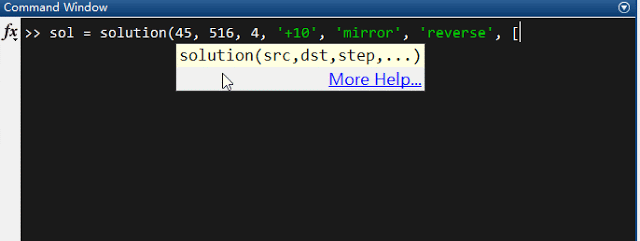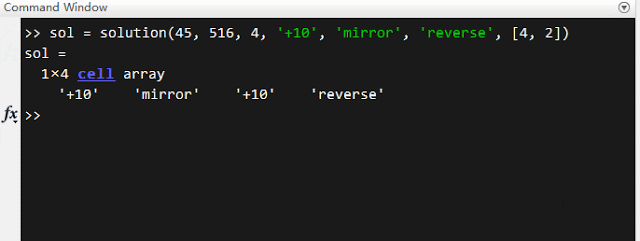
思路
基本思路是遍历求解空间,此时需要解决两个主要问题:
- 如何不重复的遍历求解空间?
- 如何确定一组求解策略的计算结果?
针对这两个问题,分别有如下的考虑:
- 由于步数($m$)是已知的,每一步可以选择的操作符个数($n$)也是固定的,那么全体解空间的总数也是确定的,为:$n^m$;另一方面,对于$n$进制的$m$位数总共的可能性也同样为$n^m$,因此可以将$0 \sim n^m-1$的数一一映射到$n$进制的$m$位数。Matlab中提供了10位数到任意进制的转换函数
dec2base - 另一方面,需要在已知策略的情况下,计算出最终结果并且和目标进行比对;为了实现这一功能,需要明确根据输入的操作符提取并实现相应的操作,这可以通过匿名函数实现。
综上,设计了两个函数,分别命名为parser和solution,其中parser负责解析输入的操作符,并且将所有的操作符保存到cell中;而solution负责遍历求解空间,找出可行解。
这款游戏提供的操作符列表如下:
% operator list:
% '-3': minues 3
% '+5': plus 5
% 'x2': times 2
% '/3': divides 3
% 10: add '10' at the end of current number
% '+/-': change sign
% '<<': backspace
% 'reverse': reverse number, keep negetive sign ('-') if it exists
% 'mirror': 32 -> 2332
% '5=>13': replace
% 'shift>': 231 -> 123
% '<shift': -150 -> -501
% '[+]2': increase each number of operators 2 (e.g. +3 -> +5)
% 'sum': 1023 -> (1+0+2+3) -> 6
% 'x^3': power
% 'inv10': 1250 -> (10-1, 10-8, 10-5, 0) -> 9850
% 'store': store current result as a number operator (ignore negetive)
% [4, 2]: portal indicator, 4th digital will added to the 2nd digital
% 1123 -> (123 + 10) -> 133
其他
代码是一边玩一边扩展的,以为所有的操作符都是改变当前的值,直到遇到了store这个元素,其操作规则是存储当前的值,并且变为一个数字按键,但是store本身并不消耗游戏步数;这一设定着实让我费了一番脑筋。考虑到store本身不会对当前值产生影响且不消耗步数,因此只需要考虑每一步操作之前是否需要执行store即可。而对于每一步之前都有“执行”或“不执行”两种操作,因此对于每一组策略,共可以衍生出$2^m$种可能。(注:其中包含重复或无效情况,后续分析)可以类比遍历求解空间的方法,为store添加一个m位的mask从而标记每一步之前是否需要store。
代码
项目代码参见:CalculatorSolution